5.10 Myron Aides

Having worked through the mathematics of linear-equation solving, take note of several aides provided by Myron. The first of these is ^[1], which transforms a matrix to reduced row-echelon form.

The second aide is the ability to solve linear equations presented in the form of a tuple or linear system ^[2]. That is, an expression like

can be transformed to a solution using Solve . An under-determined system like will not be transformed by Solve but can be transformed by → Parametric to the vector (-3⋅c+1-d, -3⋅c+2-d, c, d)ʋ where c and d take on roles as free variables The vector represents an infinite solution.

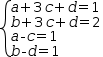
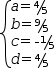
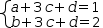
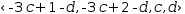
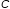
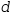
A variation on these transformations starts with various equations scattered throughout the workspace. These can be identified using multiple selection and solved directly. Of the aides mentioned here, only the solve and parametric transformations have the ability to retain variable names throughout the process. Several other transformations are used indirectly. Gather ^[3] combines scattered equations identified by multiple selection into a tuple of equations. Separate performs the inverse operation, producing individual expressions from a tuple of equations. Linear conversion produces an augmented matrix from a tuple of linear equations or produces a a tuple of linear equations from a matrix. In the latter case, names of the form x_i are generated to represent variables.

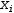
Conversion between linear-system and matrix form is performed by → Linear . Reduced row-echelon reduction is performed by Reduce . Conversion between vector and linear-surfaces forms is performed by → Parametric . Refer to Figure 3.11 to see how these transformation interact.